
年別: 2019年
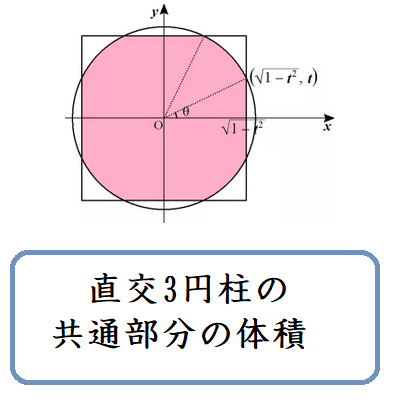
3つの直交する円柱の共通部分の体積
- 更新日:
- 公開日:
上野竜生です。今回は3つの直交する円柱の共通部分の体積を紹介します。2つのときとほぼ同様ですが計算が大変になることと,それをうまく回避する技も紹介します。もちろん大変な計算も省略せず1つ1つ丁寧に式変形して書いていきます […]

乗法定理
- 更新日:
- 公開日:
上野竜生です。確率の乗法定理を紹介します。みなさん無意識のうちに使っていると思います。 定理 <復習>条件付確率の公式 Aが起きるという条件の下でBが起きる確率は \(\displaystyle P_A(B)=\frac […]
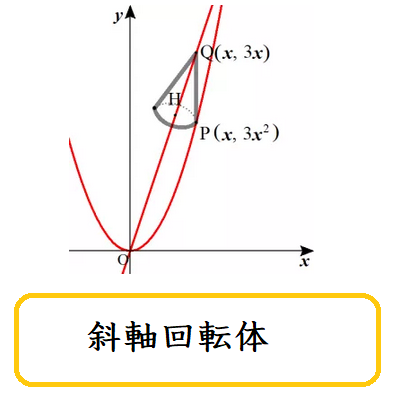
回転軸が傾いている回転体の体積
- 更新日:
- 公開日:
上野竜生です。今回は回転軸がx軸やy軸ではなく,傾いている場合の回転体の体積を計算します。 例題 f(x)=3x2,g(x)=3xとする。 (1) y=f(x)とy=g(x)で囲まれた部分をy=3xを軸に1回転させてでき […]

素数の性質・素数を利用した基本問題
- 更新日:
- 公開日:
上野竜生です。入試問題で「素数」という条件がよく出ます。素数の性質はたくさんあるのでどれを使うのか難しいですが,今回は性質をまとめてみました。役立ててください。 素数の性質 ・1とその数自身以外に正の約数をもたない整数を […]

積分の難問は誘導を利用せよ!
- 更新日:
- 公開日:
上野竜生です。積分は非常に奥が深くノーヒントで試験時間中に解くのは難しいものもあります。しかしそういう場合はたいてい(1)などでヒントが与えられています。今回は(1)などのヒントを使って(2)の難問積分を解く方法を紹介し […]

n!はmで何回割り切れるか問題
- 更新日:
- 公開日:
上野竜生です。○!は△で何回割り切れるか?というタイプの問題を解説します。 パターン1 基本(mが素数の場合) 100!は2で何回割り切れるか? 答え1から100までの中に 2で割り切れるものは50個ある。(この時点で5 […]
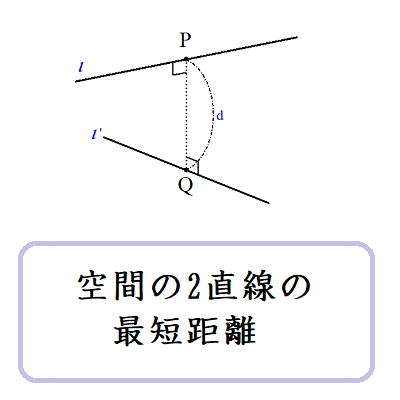
空間の2直線の最短距離
- 更新日:
- 公開日:
上野竜生です。ねじれの位置にある空間上の2直線上にそれぞれ点P,QをとったときのPQの最小を考えましょう。 裏技 共通接線 2直線l,l'はねじれの位置にあるとする。l上に点P,l'上に点QをとるときPQの最小値を求めた […]
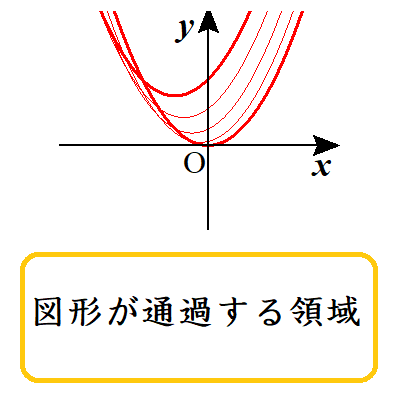
図形が通過する領域の求め方
- 更新日:
- 公開日:
上野竜生です。tやaを動かしたとき直線や曲線が通過する領域の図示の仕方を紹介します。 アイデア y=(tを含んだxの式)がある。tを実数全体で動かしたとき通過する領域を求めたい → tについて整理する。つまりtが変数,x […]

頻出!(x+y,xy)の動く領域
- 更新日:
- 公開日:
上野竜生です。今回は有名問題を紹介します。一見簡単ですが落とし穴があり,入試頻出問題で一般的な参考書でも紹介されている問題です。 実数x,yがx2+y2≦1を満たしながら動くとき、(x+y,xy)の動く領域を図示せよ。 […]

aのb乗をNで割った余り
- 更新日:
- 公開日:
上野竜生です。abをNで割った余りを求める問題を解いてみます。 「余り」の別表現 小学校では30÷7=4あまり2などと表現しましたが一般に N÷a=bあまりrであることを次のように表現することができます。 N=a・b+r […]
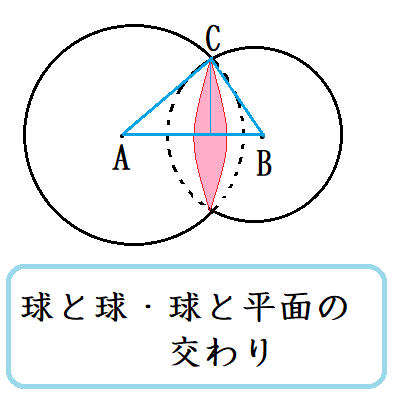
球面と球面の共通部分、球面と平面の共通部分
- 公開日:
上野竜生です。今回は球面と球面の共通部分に関する問題と、球面と平面の共通部分に関する問題を扱います。私立大学など1問の重み(配点)が低い問題をたくさん出題する大学ではよく聞かれます。難関大国公立大学のような1問が高配点の […]



