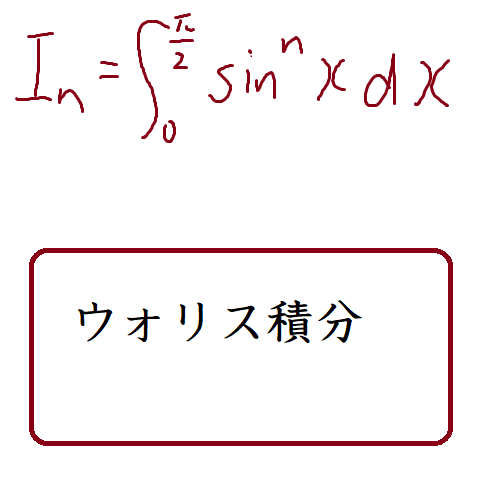数III積分の応用です。高校数学で1番面白い分野ですし大学1年の内容と被ってたりしますし入試超頻出です。ここを見ずに入試を受けるというのは不合格になりにいってるようなものです。
数III 積分の応用
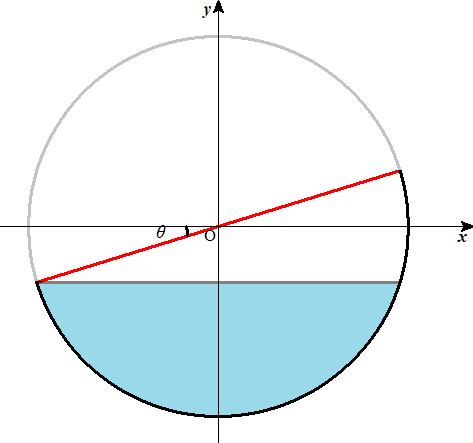
回転体の容器に水を入れる問題
- 公開日:
上野竜生です。今回は回転体の容器に水を入れる問題を紹介します。最後は簡単な微分方程式を解くことになるのでその練習も兼ねてやりましょう。(微分方程式が入試範囲外なら最後の[B]は省略してください。) 例題1 半径1の半球 […]

交点が求まらない面積の二等分に関する問題
- 公開日:
上野竜生です。今回は交点の座標が求まらない面積の問題を扱います。積分をするには交点の座標がいりますがそれが求められなくても面積がわかることがあります。 k>0とする。y=cosx \( (0\leq […]
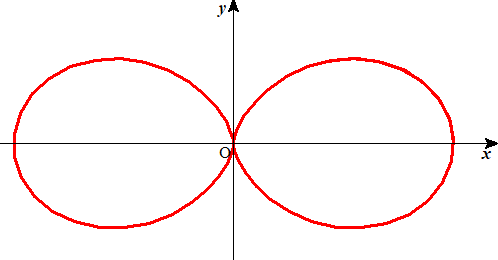
媒介変数・極座標で表された領域の面積
- 公開日:
上野竜生です。今回は媒介変数・極座標で表された領域の面積を求めます。面積の公式についてはこちらのまとめページで確認してください。 例題 極方程式 r=1+cos2θで囲まれる面積を求めよ。 グラフを求める […]
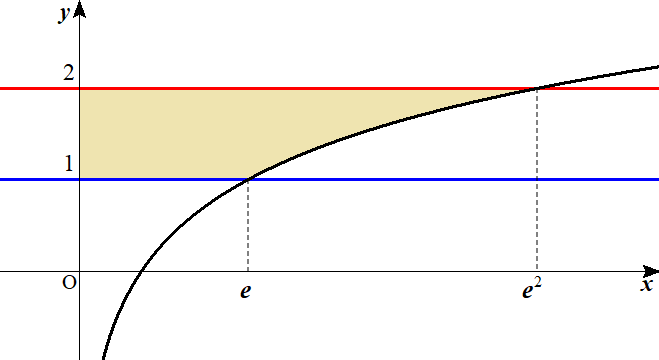
yで積分する図形の面積
- 公開日:
上野竜生です。今回は図形の面積を積分で求めるもののうちyで積分するタイプを扱います。考え方はxのときと全く同じです。数IIのときは多項式なのでyで積分するメリットは全くありませんが数IIIになるとyで積分する方が楽なもの […]
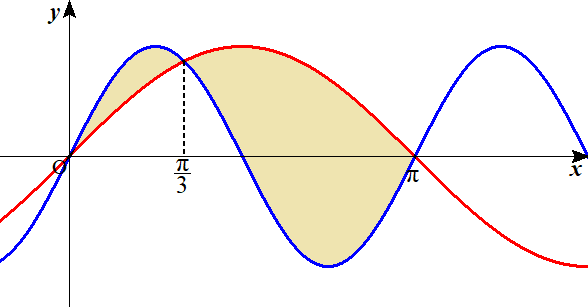
xで積分する図形の面積(数III積分)
- 公開日:
上野竜生です。今回は数IIIの面積の求め方でx軸で積分する通常のタイプの具体例を取り扱います。基本的にグラフがかけることが前提になっています。わかりやすくするためグラフをつけていますがこれを自分で書くことを心がけましょう […]
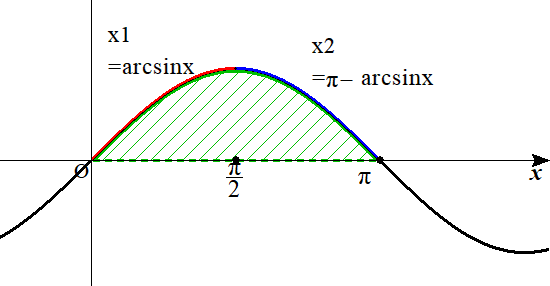
y軸まわりの回転体の体積の計算の具体例
- 更新日:
- 公開日:
上野竜生です。y軸周りの回転体の計算方法は述べましたが具体例でいろんな方法で計算してみましょう。すごく単純な例なので有名問題ですがその分いろいろな解法を見比べれると思います。 問題 \( y=\sin{x} (0\leq […]
数III積分方法と結果 標準~応用まとめ
- 公開日:
上野竜生です。今回は数IIIの積分の計算方法をまとめてみました。定石どおりにいかない積分ももちろんありますがそれは入試ではあまり問われません。 (1)まずは可能な限り複雑な部分を展開・有理化・ […]

定積分の不等式の証明
- 更新日:
- 公開日:
上野竜生です。定積分の値を具体的に求めるのではなく「○以上であることを証明せよ」といった出題もあります。このタイプはアイデアはわかりやすいですが具体的にどうするかは非常に難しく経験も必要です。 アイデア 基本は \(g( […]
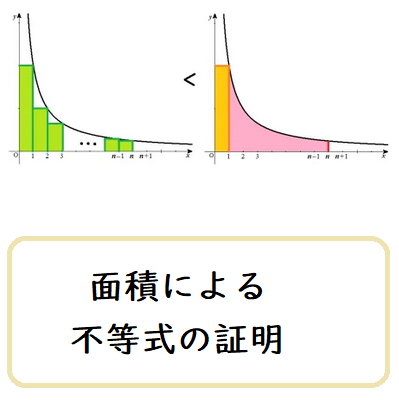
面積による不等式の証明
- 公開日:
上野竜生です。今回は数列の和の不等式の証明で面積を使って積分するものを紹介します。題材はオイラー定数に関係する有名事実です。 例題 (1) \(\displaystyle \log{(n+1)} < \sum_ […]

定積分の微分(やや複雑な場合)
- 更新日:
- 公開日:
上野竜生です。今回は定積分であらわされた関数の微分を扱います。定積分の中に微分する文字xなどが入っていない場合は明らかに微分すると0ですが積分区間にxが入っている場合を解説します。 例題 (1) \(\displayst […]

積分方程式(数IIIレベル)
- 更新日:
- 公開日:
上野竜生です。積分方程式の上級編として数IIIレベルの積分方程式を扱います。やり方はほぼ数IIのときと同じですがかなり難しく感じると思います。 復習 積分方程式の解き方(基本) ・\( \displaystyle \in […]

三角関数の直交性(sinnxcosmxの積分)
- 更新日:
- 公開日:
上野竜生です。 基本的な積分計算はできるようになった人のための応用例として三角関数の直交性を紹介します。本格的にやると大学で習うレベルですが簡単な例だと高校範囲で十分できるので入試にもたまに出ます。 三角関 […]