
2次試験対策

○の倍数判定法まとめ
- 更新日:
- 公開日:
上野竜生です。○の倍数の問題は本来中学入試レベルですが,大学入試でも場合の数の問題などでたまに出るので紹介します。基本的に証明はほぼワンパターンです。 2・4・8の倍数 2の倍数 下1ケタが2の倍数 4の倍数 下2ケタが […]
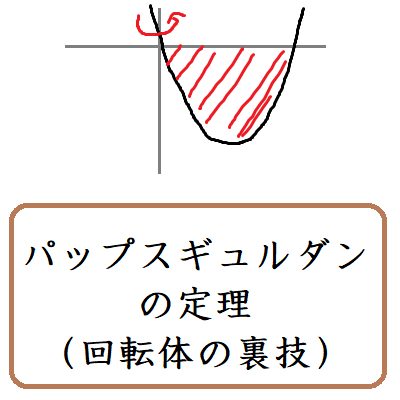
パップス・ギュルダンの定理(回転体の体積の裏技)
- 更新日:
- 公開日:
上野竜生です。回転体の体積を求める方法の裏技,パップスギュルダンの定理を紹介します。検算に使う程度にし,できる限り記述の試験では使わないようにします。 パップスギュルダンの定理 回転体の体積=回転させる面積 […]
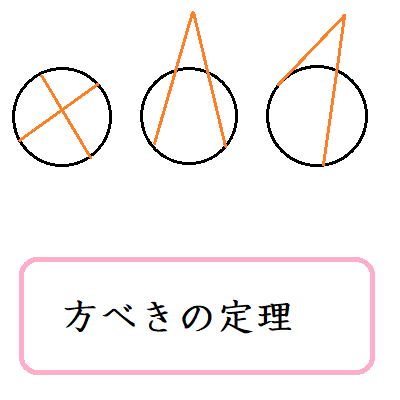
方べきの定理
- 更新日:
- 公開日:
上野竜生です。方べきの定理の3パターンとその証明をつけて,実際に練習問題を解いてみましょう。 方べきの定理1 円周上に点A,B,C,Dをとり,ACとBDの交点をEとする。このとき AE・CE=BE・DEが成り立つ。 [証 […]
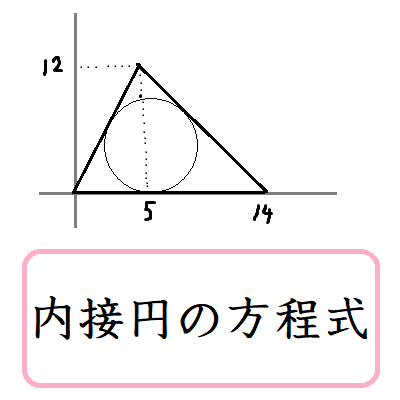
三角形の内接円の方程式の求め方
- 更新日:
- 公開日:
上野竜生です。三角形の内接円の方程式の求め方を紹介します。 三角形の内接円の方程式を求める3つの考え 内接円の性質を利用します。 1) 3つの内角の2等分線の交点が内心である。 […]

sinX=sinYなどの方程式の解き方
- 更新日:
- 公開日:
上野竜生です。sinX=sinYなどのタイプは単位円をかいて簡単に解くことができます。その解法を紹介します。 sinX=sinY 明らかにX=Yのとき等号成立します。また2π周期なのでY=X+2nπのときも成立します。 […]
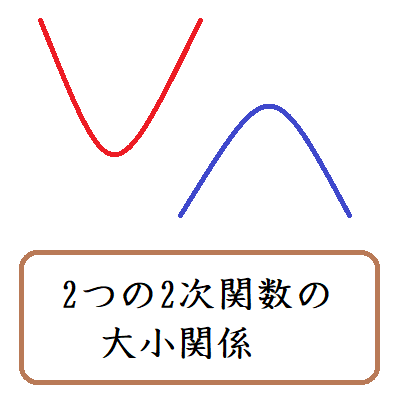
2つの二次関数の大小関係
- 更新日:
- 公開日:
上野竜生です。2つの二次関数についての大小の問題で少し注意しておきたいタイプを紹介します。 例題の(1)と(2)の違いを理解しよう 例題: f(x)=x2+2x+3とg(x)=-x2+kがある。 (1) すべての実数xに […]

複2次式(x^4+ax^2+b)の因数分解
- 更新日:
- 公開日:
上野竜生です。複2次式と呼ばれるものの因数分解を教えます。 複2次式とは xの4次式であり,かつ3次,1次の係数が0であるものです。つまり Ax4+Bx2+C の形のものです。この解き方は比較的思いつきやすいパターンと, […]
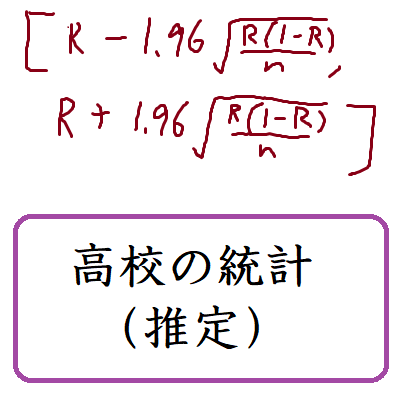
統計(高校範囲の推定のやり方)
- 更新日:
- 公開日:
上野竜生です。以前は数Cに統計が,最近では数Bに選択で統計がありますが今後は必修になるとのうわさもあります。今回は統計の中でもおそらく最後に扱うであろう推定について書いていきます。 言葉の意味を理解しよう 調査全体の集団 […]

複数の文字の因数分解は次数の低いものについて整理せよ
- 更新日:
- 公開日:
上野竜生です。1変数ではなくしかも対称式でもなく,たすき掛けでもないような式の因数分解の方法を勉強しましょう。たとえばxについては3次式,yについては2次式のときxで頑張るかyで頑張るかで難易度は圧倒的に違うのです。 原 […]

部分分数に分解する方法
- 更新日:
- 公開日:
上野竜生です。部分分数に分解すれば数学の問題が解きやすくなることが多いです。いくつか例題を出します。 例題1 次の式が成り立つように定数a,bの値を定めよ \( \displaystyle \frac{1}{x(x+1) […]
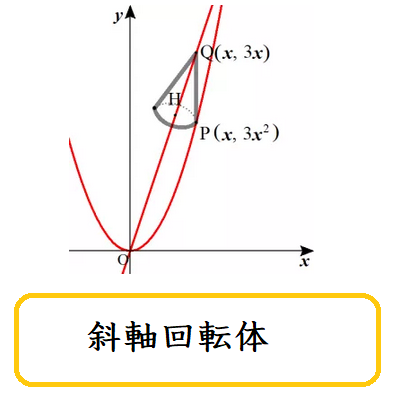
回転軸が傾いている回転体の体積
- 更新日:
- 公開日:
上野竜生です。今回は回転軸がx軸やy軸ではなく,傾いている場合の回転体の体積を計算します。 例題 f(x)=3x2,g(x)=3xとする。 (1) y=f(x)とy=g(x)で囲まれた部分をy=3xを軸に1回転させてでき […]
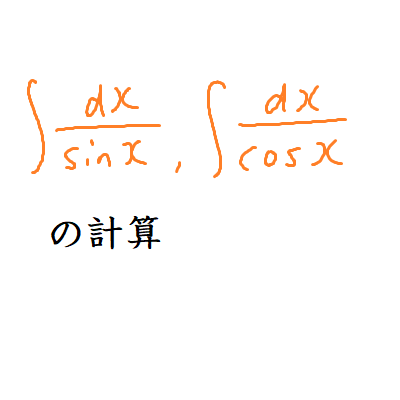
∫1/sinx dxや∫1/cosx dxの計算
- 更新日:
- 公開日:
上野竜生です。\(\int \frac{1}{\sin{x}}dx , \int \frac{1}{\cos{x}}dx \)の計算は今まで通り計算できますがこの2つを2パターンで解いてみたいと思います。 \( \dis […]
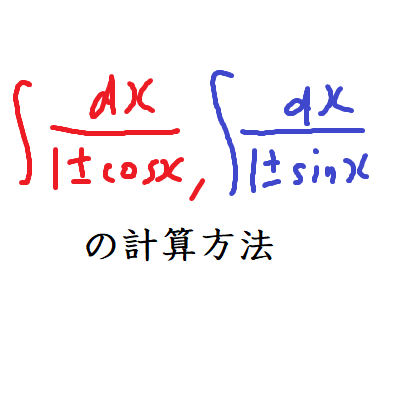
∫1/(1+cosx)dx , ∫1/(1+sinx)dxなどの計算
- 更新日:
- 公開日:
上野竜生です。今回は \( \int \frac{1}{1+\cos{x}}dx , \int \frac{1}{1-\cos{x}}dx , \int \frac{1}{1+\sin{x}}dx , \int \fra […]
3次関数の性質まとめ
- 更新日:
- 公開日:
上野竜生です。2次関数はいろいろな性質がありますが、3次関数も比較的性質が限られています。なのでここでまとめておきましょう。 なお3次関数を\( f(x)=ax^3+bx^2+cx+d \)とおきます。 a […]
