数Aの場合の数と確率を扱います。
数A 場合の数と確率

正十二角形の3点を結んでできる三角形の個数(種類別)
- 更新日:
- 公開日:
上野竜生です。正n角形のn個の頂点の中から3つの点を結んでできる三角形の個数についての問題は私立大学でたまに見かけます。頻出の十二角形の場合で徹底的に調べておきます。 問題 正十二角形A1A2A3・・・A1 […]
x+y+z=nとなる自然数の個数
- 更新日:
- 公開日:
上野竜生です。今回はx+y+z=nとなる自然数や非負整数の組の個数について紹介します。やることは組み合わせ計算ですが,問題の言い換えがかなり独特で,一度経験しないとひらめかないと思うので1度見ておきましょう。 問題 (1 […]
立体の色の塗り分け方は何通り?
- 更新日:
- 公開日:
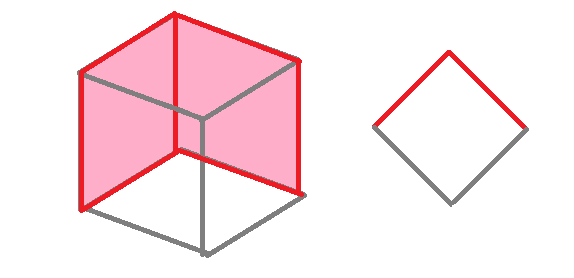
上野竜生です。今回は立体の色の塗り分け方が何通りあるか紹介します。基本的には回転して同じになるかどうかを意識するのが重要で,普通の順列をつかうのか円順列を使うのかしっかり見極めましょう。 例題1 立方体の6面に色を塗る。 […]

場合の数 基本は全部数える!時間を短縮するための計算
- 更新日:
- 公開日:
上野竜生です。場合の数はなかなかクセがあり,苦手とする人も多いと思います。確かにここはある意味で難しいです。ややこしくなっている人のためにいくつかパターンを紹介します。 記号の理解 n!とは1からnまでの整数をすべてかけ […]
余事象を利用した場合の数の求め方
- 更新日:
- 公開日:
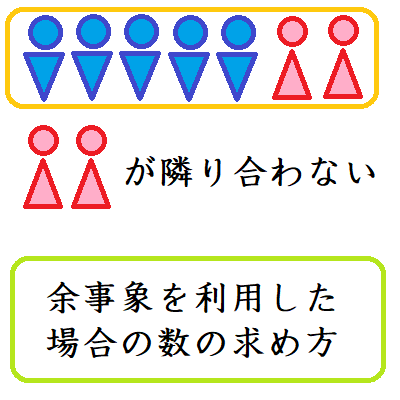
上野竜生です。余事象を利用して場合の数を求めてみましょう。 基本 普通に求めるのが大変そうな場合は全体の数から条件に当てはまらない場合の数を引けば条件に当てはまる場合の数が求まる。 例題1 「1」「2」「3」「4」「5」 […]

○の倍数は何通りできるか問題
- 更新日:
- 公開日:
上野竜生です。数字の並べ替えで○の倍数が何通りあるかの問題を紹介します。 例題 「0」「1」「2」「3」「4」から3枚を選んで3桁の整数を作る。なお先頭に0がくるもの、たとえば012は2桁の整数12とみなす。 (1) 3 […]

組にわける方法は何通り?
- 更新日:
- 公開日:
上野竜生です。組に分ける方法は何通りあるかの問題について解説します。微妙なニュアンスの違いで答えが変わってくるので注意が必要です。 重要なのは区別できるかできないか 具体例は下の例題のようなものを参考にしてください。基本 […]
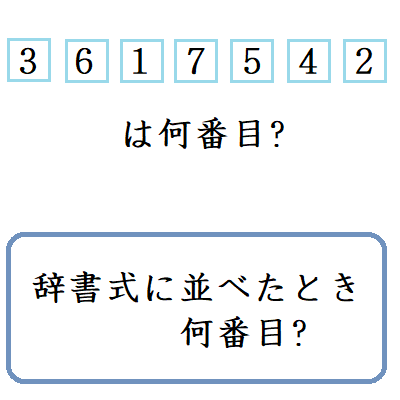
辞書式に並べたとき何番目問題
- 更新日:
- 公開日:
上野竜生です。数字を並べ替えたり文字を辞書式に並べ替える場合の問題を解説します。 数字の並べ替え 「1」「2」「3」「4」「5」「6」「7」の7つの数字を並べ替えてできる5040個の数字を小さいほうから順に並べ替える。 […]
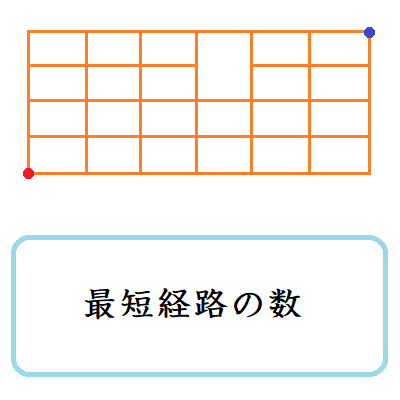
最短経路は何通りあるか
- 更新日:
- 公開日:
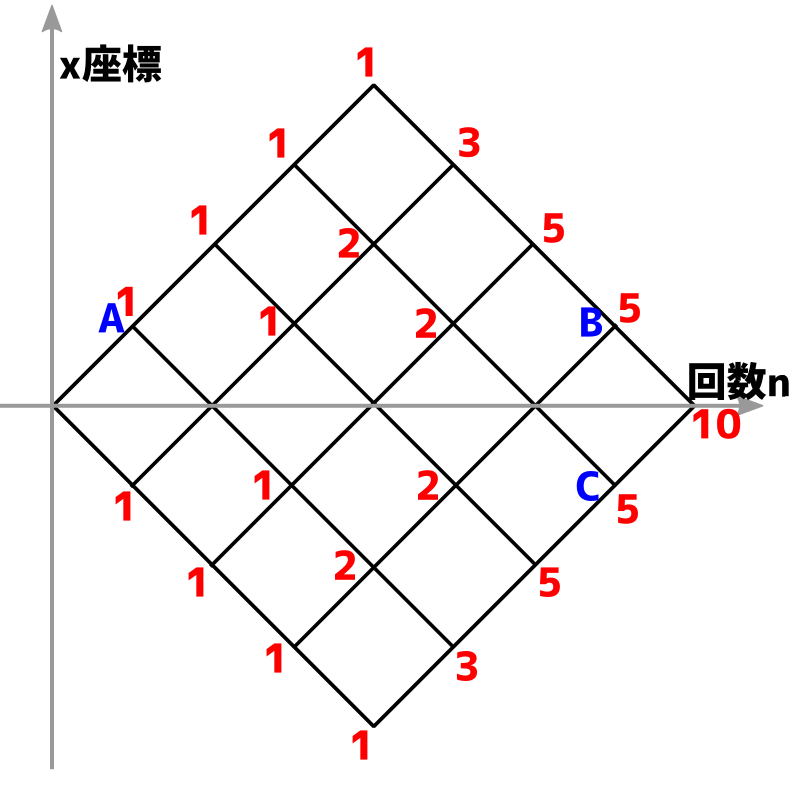
上野竜生です。図が与えられていて最短経路が何通りあるかを求める方法を紹介します。 基本 ↑に何回・→に何回いくか考える 図のような道がある。今左下の点から右上の点まで最短経路で進む。 (1) 進み方は何通りあるか? (2 […]
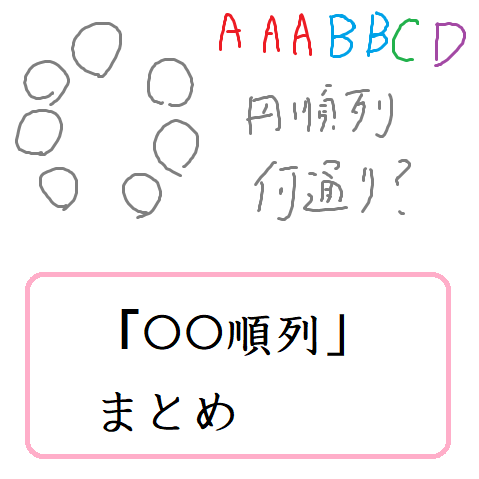
「何通りある?」○○順列まとめ
- 更新日:
- 公開日:
上野竜生です。○○順列についてまとめてみました。 順列 「1」「2」「3」・・・「n」を並べ替える方法:n!通り。 まず左端は1~nまでn個選べるのでn通り。 2番目は1番目に選んだもの以外のn-1個から選ぶのでn-1通 […]
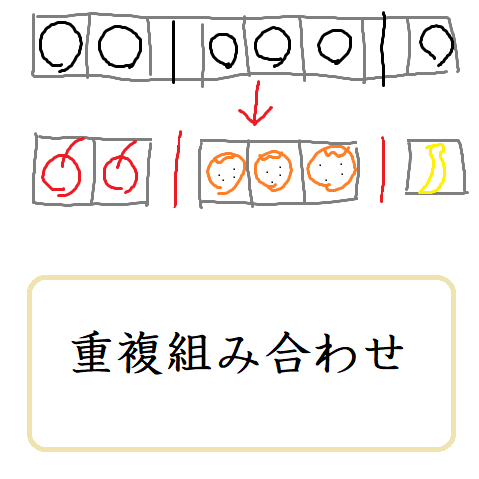
重複組み合わせは普通の組み合わせだけで計算せよ
- 更新日:
- 公開日:
上野竜生です。重複組み合わせの公式は覚えるものではありません!Hという記号は基本使わないので覚えなくてもいいでしょう。 とはいえ,一応定義は書いておきます。 nHr=n+r-1Cr n個の中から重複を許してr個選ぶやり方 […]

確率の基本
- 更新日:
- 公開日:
上野竜生です。確率の基本を教えます。よくあるような簡単なものから積み上げるタイプでもいいですがここではあえて一般化したものを使ってある程度紹介します。 いきなりですがまず最初に次の公式を教えます! POINT事象Aが起き […]

和事象の確率
- 更新日:
- 公開日:
上野竜生です。確率の基本となる和事象の確率と,そこから派生される確率の和を勉強していきましょう。 前回に引き続き,使う公式は次の通り。 POINTAが起こる確率をP(A),Bが起こる確率をP(B),AかつB […]

反復試行の確率の求め方
- 更新日:
- 公開日:
上野竜生です。確率の計算の1つ,反復試行の確率の計算方法を理解しましょう。 公式 先に公式を見せます。 POINTある事象が起きる確率がpである試行をn回行うとき,ちょうどk回の事象が起きる確率は \(\displays […]