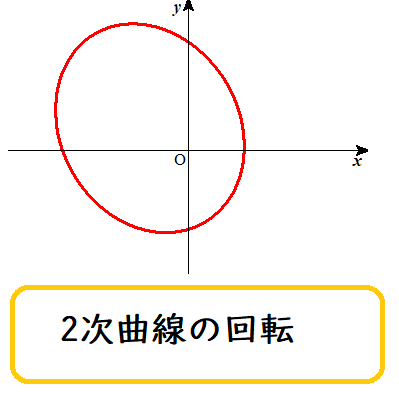
2次試験対策

条件付き確率
- 更新日:
- 公開日:
上野竜生です。今回は条件付確率について紹介したいと思います。 公式 Aがおきるという条件の下でBがおきる条件付確率は\(\displaystyle \frac{P(A\cap B)}{P(A)}\) 分母はAが起きる確率 […]
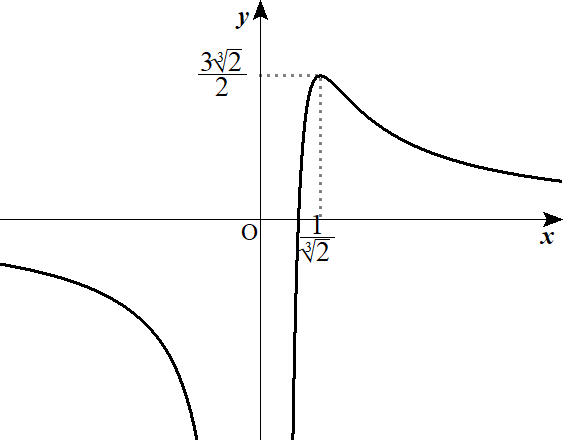
関数が接する条件・共通接線の本数(数III範囲)
- 公開日:
上野竜生です。今回は接線に関する問題を紹介します。共通接線と接線の本数は入試に出題されてもいいぐらいの難易度ですのでここまで勉強すれば入試で戦えるようになってきます。数IIレベルのものは共通接線の求め方で復習してください […]

2変数2次式の最大最小の求め方
- 更新日:
- 公開日:
上野竜生です。制約条件がなく1変数にならないタイプの2変数2次式の最大・最小の求め方を紹介します。 基本は平方完成するだけです! 2か所で平方完成して両方の( )2の中身が0になるところが最小という考えです。 例題1 x […]

指数関数の最大最小の求め方
- 更新日:
- 公開日:
上野竜生です。指数関数の最大・最小の求め方を教えます。 基本:2xなどをAとおいて多項式などに帰着させる 例題: 4x-2x+1の最小値を求めよ。 2x+1=2・2xに注意します。 答え2x=A(A>0)とおく。 […]

対数関数の最大最小の求め方
- 更新日:
- 公開日:
上野竜生です。対数関数の最大最小の求め方を練習しましょう。 パターン1:logaf(x)の形にするとf(x)の最大最小に帰着できる logaf(x)の最大最小はf(x)の最大最小と深い関係があります。 a>1のとき […]

対数関数の領域図示問題
- 更新日:
- 公開日:
上野竜生です。対数関数の領域を図示する問題です。特に新しいことはありませんがこれまでの対数の性質を使い,場合分けも複雑なので自力で解くのは難しいです。例題を1問だけ載せているので解けるか挑戦してみましょう! 例題 \(\ […]
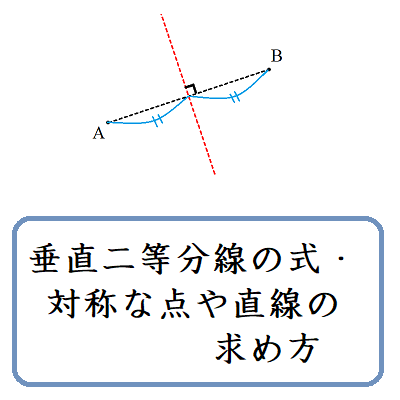
垂直二等分線の式・対称な点や直線の求め方
- 更新日:
- 公開日:
上野竜生です。対称移動させた点や直線の求め方を紹介します。入試でもよく「~を対称移動させたものをC'とする。」のように序盤で計算させる内容の一つであり,ここで躓くと大問全体を捨てるハメになってしまいます。 今回使う知識 […]
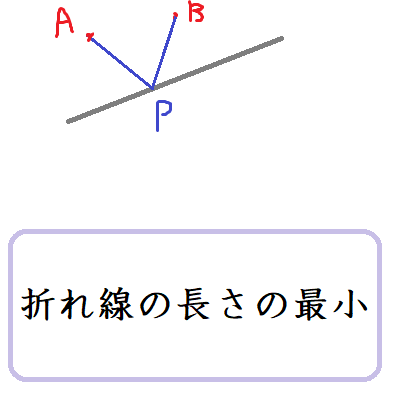
2つの線分の長さの和の最小値
- 更新日:
- 公開日:
上野竜生です。折れ線の長さの和の最小値を求める問題は試験でよく出ます。定石を知らないと膨大な計算量になるので知っておきましょう。 例題1 A(0,1), B(6,2)がある。x軸上に点Pを、線分の長さの和AP+PBが最小 […]
点と直線の距離の公式
- 更新日:
- 公開日:
上野竜生です。点と直線の距離の公式は微妙に間違えやすく、差がつきやすいです。応用もできるので苦手な人は見ておきましょう。 点と直線の距離の公式 点\( (X,Y) \)と直線\( ax+by+c=0 \)の距離は \( […]
極限が与えられたとき、未知数(係数や指数部分)を求める
- 公開日:
上野竜生です。今回は極限計算の結果から未知数を求める問題の解法を紹介します。例題1・2のような係数部分を求めるのも重要ですが例題3のようなタイプが難関大入試によく出題されます。 例題1 \(\displaystyle \ […]
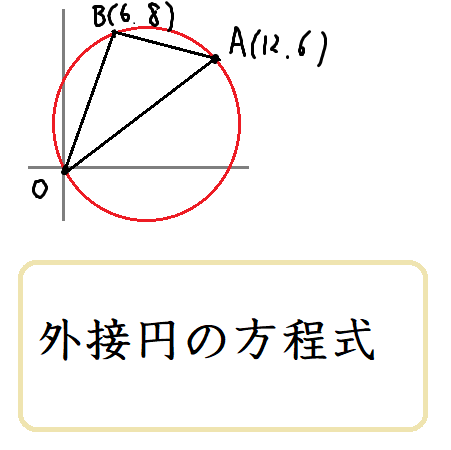
外接円の方程式の求め方
- 更新日:
- 公開日:
上野竜生です。図形問題でどうしても解けなくなったら座標で解くことになりますが今回はその中で外接円の方程式を正確に計算する方法を紹介します。 外接円の方程式の特徴を掴んで計算する! […]

数列の和(偶奇で場合分けするパターン)
- 更新日:
- 公開日:
上野竜生です。奇数項と偶数項でパターンが違う数列の和を求めてみます。 例題 nが偶数のときan=2n, nが奇数のときan=0とする。\( \displaystyle S_n = \sum_{k=1}^n a_k \)を […]
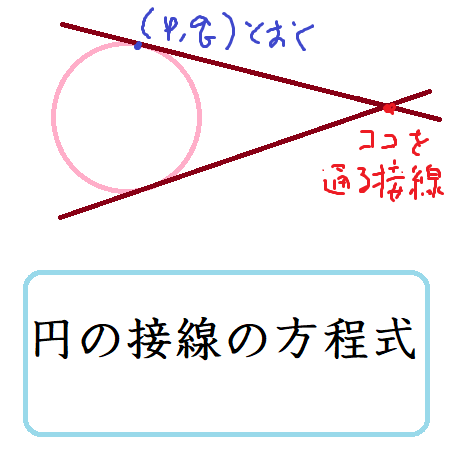
円の接線の方程式の導出方法
- 更新日:
- 公開日:
上野竜生です。円の接線の方程式を導出する方法を紹介します。 円の接線の公式 円(x-a)2+(y-b)2=r2の円周上の点(p,q)に対する接線の方程式は (p-a)(x-a)+(q-b)(y-b)=r2である。 覚え […]
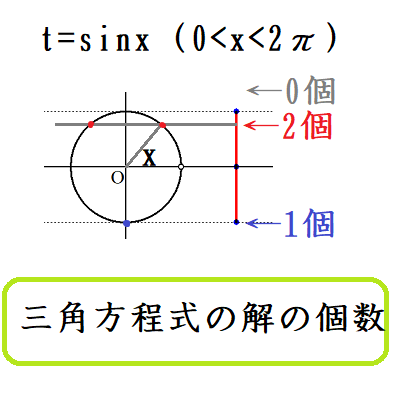
三角方程式の解の個数 tの個数とxの個数の対応を考えよ!
- 更新日:
- 公開日:
上野竜生です。三角関数の方程式の解の個数を求める問題ではt=(三角関数)とおくのが鉄則ですがtとxは1対1対応しません。そのことも考慮した解法を勉強しましょう。 tとxの対応に注意! たとえば0≦x<2πのとき,( […]
